Dynamic Issuance

As opposed to having a fixed issuance rate, the Subspace Network implements a dynamic issuance rate based on network usage, where, roughly, the inflation rate is inversely proportional to the utilization rate of the blockspace.

TLDR: The farmer who proposed a block gets some fresh SSC + fees, and voters get some fresh SSC regardless of what the proposer got.

Space Race

The rewards issuance is not enabled by default at the chain genesis. After the genesis block, several things need to happen before authoring blocks by anyone, and rewards can be enabled (See genesis algorithm). Then:

1. Define a target space pledged to the network at which the rewards will be enabled (i.e., 8PiB for Gemini-3h). In the runtime, it is defined in terms of the target value of the solution range solution_range_for_rewards.
2. Identify an assumed current space pledged initial_solution_range.
3. Enable solution range adjustment starting at initial_solution_range at the next era
4. Set in the runtime the solution_range_for_rewards below which to automatically enable rewards.
5. Enable block authoring by anyone.
6. Farmers will start producing blocks and the solution range will be updated every era as defined in Solution Range Updates
7. Eventually, as farmers pledge more space, the network’s solution range will reach a value ≤ solution_range_for_rewards at a certain block $B$.
8. The RewardsEnabled runtime item is set to true. The rewards will start to be paid to voters and proposer of the very next block.

Issuance Function

The issuance function currently consists of two components: a decaying component and a utilization-based component. The decaying component issues a constant reward for some initial interval and gradually reduces it over time. The utilization-based component issues a reward based on the average utilization of blockspace in recent blocks. Such construction allows for more decaying components to be included for additional incentivization.

Full Block

MAX_NORMAL_BLOCK_LENGTH is the byte size limit of a full block set to consensus and equal to 0.75*MAX_BLOCK_LENGTH (currently 3.75 MiB for) normal txs (different from operational (e.g., votes, equivocation) and mandatory (e.g., new archived segments))

Utilized Block Resources

AvgBlockspaceUsage (in bytes)

Item that stores the utilization of blockspace (in bytes) by the normal extrinsics used to adjust issuance. Should be ≥0 and ≤MAX_NORMAL_BLOCK_LENGTH. Blockspace utilization is computed as an exponential moving average of blockspace utilization of the last num_blocks blocks, updated every block.

num_blocks: number of the blocks over which utilization is measured, should be ≥0 (Currently, 100)

1. Compute the amount of blockspace utilized in this block used_blockspace ****as the sum of encoded lengths of normal transactions in block body.
2. For genesis block AvgBlockspaceUsage = used_blockspace=0
3. If num_blocks==0 , return the used_blockspace of the current block.
4. Else if block_height <= num_blocks, store new value (AvgBlockspaceUsage + used_blockspace)/2
5. After block_height > num_blocks, use multiplier = 2/(num_blocks+1) Store new value multiplier * used_blockspace + (1-multiplier) * AvgBlockspaceUsage

Issuance Components

We define a base block issuance as the number of tokens issued per block in a static case: a fixed reward to block proposer and EXPECTED_VOTES_PER_BLOCK voters.

RemainingIssuance: tokens left to issue to farmers at any given time

We define a reward split rule where the block proposer and voters are entitled to a share of the base reward:

• proposer_share = 1
• voters_share, currently =EXPECTED_VOTES_PER_BLOCK (for gemini-3h)
• total_shares = proposer_share + voters_share

The total actual reward issued includes a sum of several independent issuance components, each characterized by different values of common parameters based on the value of BASE_REWARD computed off-chain beforehand as described in Off-chain Issuance curve parameters setting.

$B$ is the block starting from which the rewards component is activated. It can be set manually by an extrinsic initializing the component or automatically if rewards are subject to Space Race.

Defining a component requires setting the following parameters:

struct RewardPoint:

A reward point is a tuple of (block, subsidy). Each point is a start block of a rewards decay phase and the subsidy amount for that block. For blocks between each pair of points, we use linear approximation to compute their respective subsidies.

Block numbers have to be strictly increasing, and reward values have to be strictly decaying across all phases.

The length of this list is the number of decay phases, usually 4-6.

If a component is initialized before the rewards are activated via Space Race (i.e. at genesis), all block heights in the reward points will be offset by the block number $B$ at which rewards get activated as soon as Space Race completes. Else, if a new component is defined over pre-existing rewards, the block heights in the reward points list are offset by the block number at which the component initialization network upgrade goes through.

We currently define two such components: block proposer reference subsidy and voter reward. If desired, we may introduce other components (i.e., one to incentivize operators for an initial period of low domain activity).

(Numbers for Gemini-3h):

ProposerSubsidyPoints: vector of RewardPoints

[(0, 100000000000000000), (201600, 99989921015995728), (79041600, 92408728791312960), (779041600, 45885578019877912), (2443104160, 8687806947398648)]

The first value of subsidy here is equal to proposer_share/total_shares*BASE_REWARD, and the rest follow exponential decay, computed off-chain as described in Off-chain Issuance curve parameters setting. The points describe the following phases:

• decay phase 0: 0 ≤ block height < 201600, subsidy 100000000000000000 -> 99989921015995728
• decay phase 1: 201600 ≤ block height < 79041600, subsidy 99989921015995728 -> 92408728791312960 decay phase 1
• decay phase 2: 79041600 ≤ block height < 779041600, subsidy 92408728791312960 -> 45885578019877912 decay phase 2
• decay phase 3: 779041601 ≤ block height < 2443104160, subsidy 92408728791312960 ->8687806947398648)]
• decay phase 4: 2443104160 ≤ block height, constant subsidy of 8687806947398648 until remaining issuance runs out.

VoterSubsidyPoints: vector of RewardPoints

[(0, 100000000000000000), (201600, 99989921015995728), (79041600, 92408728791312960), (779041600, 45885578019877912), (2443104160, 8687806947398648)]

The first value from_subsidy is the initial subsidy equal to voter_share/total_shares*BASE_REWARD, and the rest follow exponential decay, computed off-chain as described in Off-chain Issuance curve parameters setting

Based on those parameters, a function deterministically computes the amount of new SSC to be issued via a specific component

Once an issuance component has been initialized, the issued reward for each individual block will be computed using linear approximations for as many decay phases as there are pairs of points listed in …SubsidyPoints.

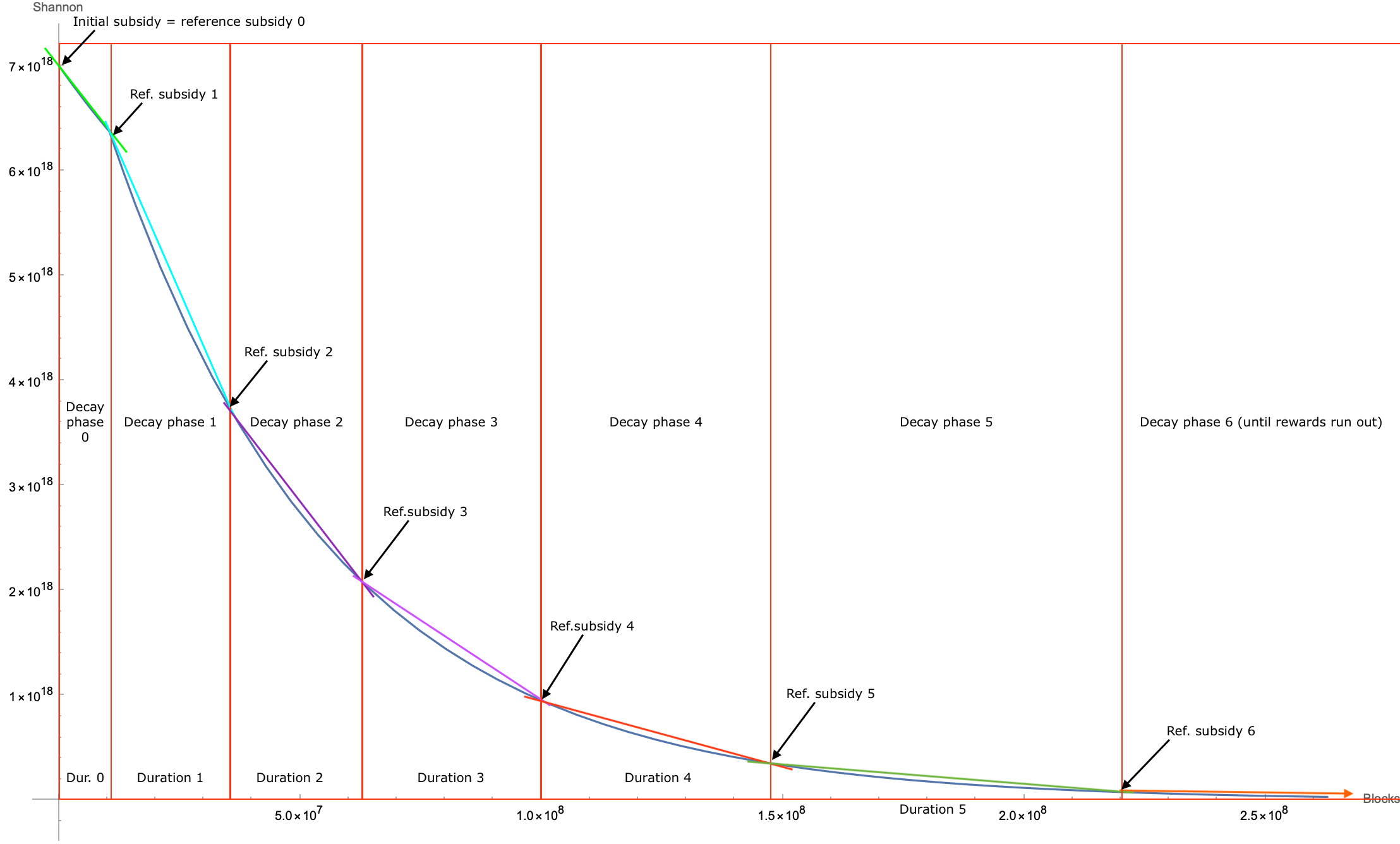
Figure 1

reference_subsidy_for_block(points: Vec<RewardPoints>, block_height) → Balance

1. Ensure points list is well-formed: both block numbers are strictly increasing and subsidies are strictly decreasing.

2. If block_height< $B$ or rewards are not enabled yet, return 0.

3. Identify the decay phase in which this block belongs in points: find a pair of points in a sliding window manner, such that first point block ≤ block_height AND next point block > block_height. The first point will be referred to (from_block, from_subsidy), and the second point (to_block, to_subsidy).

   Return from_subsidy - (from_subsidy - to_subsidy) / (to_block - from_block) * (block_height - from_block)

4. (Tail issuance, may or may not be 0) If none of the defined phases match, block_height > points.last().block, return points.last().subsidy

Total Issued Reward

By total issued reward, we mean SSC newly issued by the protocol when a new block is proposed, separate from transaction fees paid with existing credits. The total reward is higher when blocks are underutilized and lower when blocks are fuller.

The effective issued reward may be less than the BASE_REWARD if block utilization is above 0, or the voters are few. On full utilization, no reward is issued to the proposer. However, voters’ subsidy remains intact.

The effective total reward is the sum of all issued rewards is block_reward(block_height) + num_votes*vote_reward(block_height)

The effective reward is subtracted from RemainingIssuance every block.

Proposer gets a cut of voting rewards to incentivize them to include votes (which take up blockspace and don’t pay for storage). PROPOSER_TAX_ON_VOTES = 1/10 The effective proposer reward is: block_reward(block_height) + PROPOSER_TAX_ON_VOTES * num_votes * vote_reward(block_height)

Block Reward

By block rewards we mean SSC newly issued by the protocol to the farmer who proposed the block (proposer). The farmer also gets all the fees for transactions in the block in addition to this reward. In fuller blocks, the sum of fees earned by the block proposer should be higher than their share of the block reward. This ensures farmers are incentivized to fill the blocks with tx rather than relying on newly issued credits.

block_reward(block_height) → Balance

The reward to be issued to the proposer for this block is defined by a reward function and computed for each block using latest AvgBlockspaceUsage, transaction_byte_fee and block_height.

reference_subsidy-blockspace_utilization*min(reference_subsidy,max_block_fee)

where

reference_subsidy = reference_subsidy_for_block(ProposerSubsidyParams, block_height)

max_block_fee = MAX_NORMAL_BLOCK_LENGTH * transaction_byte_fee

blockspace_utilization=AvgBlockspaceUsage/MAX_NORMAL_BLOCK_LENGTH

Voting Reward

By vote rewards we mean SSC newly issued by the protocol to incentivize voting to each voter.

Vote rewards have a probabilistic issuance rate based on expected number of votes in the block. Reward numbers defined in VoterSubsidyParams are issued per vote with all voters getting equal reward.

vote_reward(block_height) → Balance

reference_subsidy_for_block(VoterSubsidyParams, block_height)

90% of the vote_reward are accredited to the voter account and 10% to the proposer.

Off-chain Issuance curve parameters setting

For Gemini-3h the following initial parameters are used to set the issuance curves for both proposer and voter rewards (the are the same in gemini-3h, but generally don’t have to be):

• BASE_REWARD = 1 SSC
• proposer_share = 1
• voters_share = EXPECTED_VOTES_PER_BLOCK
• total_shares = proposer_share + voters_share
• RemainingIssuance = $10^9$ SSC
• initial_subsidy: voters_share/total_shares/EXPECTED_VOTES_PER_BLOCK*BASE_REWARD = proposer_share/total_shares*BASE_REWARD = $10^{17}$ Shannon
• max_issuance = $10^8$ SSC: 10% of remaining issuance at component initialization time

The total issuance curve (green) is a sum of 2 exponential components: component 1 (blue) starts to decay immediately, component 2 that has flat issuance for a while and starts to decay later. Without loss of generality both curves are assumed to start issuance at block 0. After deployment to gemini-3h the block numbers are shifted with respect to how many blocks were already produced.

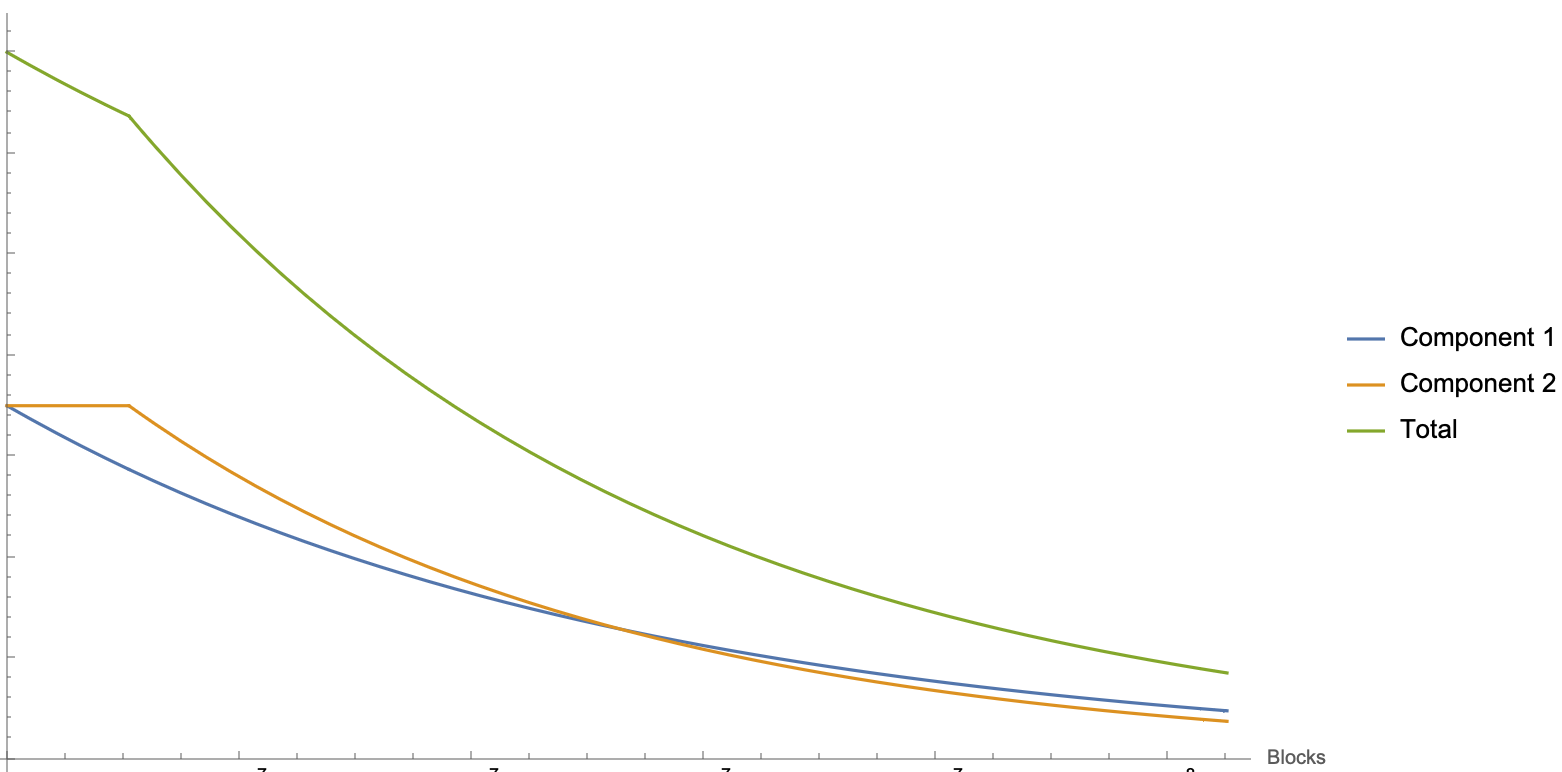Figure 2

To be able to use linear approximations in different decay phases (as illustrated in Figure 1), we need to compute certain checkpoint values of reference subsidy on the green curve. For Gemini-3h, we have identified the following start blocks of decay phases:

1. $h_1=201 600$
2. $h_2=h_1+ 78 840 000=79041600$
3. $h_3=h_2+700000000=779041600$
4. $h_4=h_3+2 365 200 000 =2443104160$

To compute the required subsidy values on the green curve, we used the following algorithm:

1. Set the individual components exponential decay starts decay_start_block1 = 0 decay_start_block2 = subsidy_durations[0] = $201600$
2. Split the issuance budget between 2 exponential components:
   1. max_decay_issuance1 = max_issuance/2 = $5*10^7*10^{18}$ Shannon
   2. max_decay_issuance2 = max_issuance/2 - subsidy_durations[0] * initial_subsidy/2= $5*10^7*10^{18}-201600*10^{17}/2=49989920*10^{18}$ Shannon
3. Set decay curve parameters:
   1. k1=initial_subsidy/2/max_decay_issuance1 = $10^{17}/2/(5*10^7*10^{18})=1/10^9$
   2. k2=initial_subsidy/2/max_decay_issuance2 **= $10^{17}/2/(49989920*10^{18})=1/999798400$
4. For each decay phase start block $h_i$ compute rounded down to nearest integer

$$f(h_i)=\text{initial\_subsidy}/2*(e^{-k_1*h_i}+e^{-k_2*(h_i-\text{decay\_start\_block\_2})})$$

$f(h_1)=99989921015995728$

$f(h_2)=92408728791312960$

$f(h_3)=45885578019877912$

$f(h_4)=8687806947398648$