Cryptographic Primitives
The following primitives are used in various parts of the protocol.
Hash
Hashes provide succinct commitments to arbitrary data.
hash(message) generally denotes BLAKE2b-256 unless otherwise specified.
keyed_hash(key, message) denotes keyed BLAKE2b-256 hash.
Substrate primitives (i.e., block hashing) use BLAKE2b-256 as well.
Proof-of-Space primitives use BLAKE3.
Merkle Tree
Provides succinct commitments (Merkle roots) to arbitrary-sized data sets with efficient proofs (witnesses) of inclusion. Current usages include trees for:
- extrinsics sets in blocks (as defined in the Substrate framework)
- state of the blockchain (as defined in the Substrate framework)
- execution trace for the domain block
Merkle Mountain Range (MMR)
Provides succint commitments to arbitrary-sized data sets with efficient proofs (witnesses) of inclusion, updates and lookups. Specifically on the consensus chain, the Merkle Mountain range commits to the state of the chain. Specific block data is pruned from the consensus runtime state as the chain progresses, but the Merkle Mountain range allows for efficient verification of the pruned state. MMR proofs are primarily used in cross-domain messaging and fraud proofs.
We currently use Substrate pallet-mmr as a primitive type and we add another wrapper to provide LeafData on every block. A new MMR leaf is added during new block initialization, and each leaf from a given block holds information of the previous block.
MMR uses Keccak256 as the hashing function for greater interoperability with other chains.
Pallet implementation
struct LeafData
The leaf data for the Merkle Mountain Range contains the following fields:
block_numberblock_hashstate_rootthat can be used to prove specific storage after block was importedextrinsics_rootthat can be used to prove block body
leaf_data
leaf_data() -> LeafData
Fetches parent consensus block number and hash from the frame-system and fetch state root and extrinsic root through host function.
on_new_root
on_new_root(mmr_root_hash)
Implements the OnNewRoot hook for the pallet, which is triggered when a new MMR root is computed. When a new MMR root is computed, this function will deposit a log entry in the system digest with the new root hash. This allows other pallets or external systems to be notified of the new MMR root.
Runtime Integrations
mmr_root
mmr_root() -> mmr_root_hash
Returns the on-chain MMR root hash.
mmr_leaf_count
mmr_leaf_count() -> index
Return the number of MMR blocks in the chain.
generate_proof
generate_proof(block_numbers, best_known_block_number: Option) -> (Vec<Leaf>, Proof)
Generates an MMR proof for a series of block numbers. If best_known_block_number argument is provided, uses the historical MMR state at the given block height n. Else, uses current MMR state. Returns a tuple containing the list of MMR leves corresponding to block_numbers and the MMR proof.
verify_proof
verify_proof(leaves, proof) -> Ok/Error
Verifies an MMR proof against on-chain MMR for a given batch of leaves. The leaves should be sorted such that corresponding leaves and leaf indices have the
same position in both the leaves vector and the leaf indices contained in the proof. It will return Ok if the proof is valid and an Err(..) if MMR is inconsistent (some leaves are missing) or the proof is invalid.
Digital Signature
Digital signatures secure different parts of consensus by providing a means of authentication.
We currently use Schnorr/Ristretto x25519 (also known as sr25519) as the key derivation and signing algorithm (with the schnorrkel library).
Non-canonical Schnorr signatures are used to sign rewards for a newly forged block (as defined in Substrate) and votes by farmers, as well as transactions and transaction bundles by domain operators. Canonical (deterministic) signatures are used as a verifiable random function (VRF) in the slot leader election among domain operators. A canonical scheme is necessary for these cases to prevent attackers from repeatedly signing until they produce an election solution that meets the threshold (as part of a grinding attack).
sign
sign(secret_key, message) → signature
Creates non-canonical signature.
verify
verify(public_key, message, signature) → bool
vrf_sign
vrf_sign(secret_key, transcript) → vrf_signature
Runs VRF on a single input transcript, producing the vrf_output and corresponding short vrf_proof. The resulting vrf_signature is a tuple (output, proof).
vrf_verify
vrf_verify(public_key, transcript, vrf_signature) → bool
Splits vrf_signature into output and proof and verifies proof for an input transcript and the corresponding output.
Kate-Zaverucha-Goldberg (KZG) Polynomial Commitment
KZG polynomial commitment scheme allows for constant-sized inclusion proofs for arbitrary-sized data sets. Specifically:
- The commitment size is constant and equal to one group element of an elliptic group that admits pairings. With BLS12-381, that is 48 bytes
- The proof size is constant and equal to one group element (48 bytes)
- Verification time is constant and requires two group multiplications and two pairings
- Proving time (commitment and proof generation) is linear in the degree of the underlying polynomial (length of committed data)
Subspace adopted the KZG public parameters from the Ethereum KZG ceremony, leveraging the Structured Reference String (SRS), also known as the universal reference. The SRS is publicly available, allowing anyone to construct their KZG commitments with confidence in the underlying security. The success of the Ethereum ceremony guarantees the trustworthiness of the setup.
The cryptographic hash of the final parameters file, produced at the conclusion of the Ethereum KZG ceremony, serves as a digital fingerprint, ensuring the integrity and authenticity of the SRS used across the Ethereum network. This hash enables users to verify that they are working with the correct set of parameters, untouched and unaltered since their creation during the trusted setup.
Trusted Setup for KZG Commitment
The trusted setup is a critical step in the KZG commitment scheme. It requires a secret value, denoted as s, to generate the polynomial commitments. This secret is used only once during the setup phase and must then be securely discarded to ensure the integrity of the system. Possession of s after the setup allows for the fabrication of false proofs, compromising the scheme's security.
The secret value s is typically generated through a Multi-Party Computation (MPC) ceremony, ensuring that no single participant knows the secret. This process secures the value by distributing trust among multiple parties.
Ethereum's Approach to the MPC Ceremony
The Ethereum community conducted its MPC ceremony using the "Powers of Tau" method. This process begins with a participant adding their secret to the mix, computing the first polynomial, and then passing the result to the next participant. Each subsequent participant adds their secret and forwards the updated polynomial to the next, in a secure chain of contributions. The ceremony's security hinges on at least one participant keeping their contribution secret, embodying the principle of a 1-out-of-N trusted setup. This method ensures that no single entity can compromise the system.
For a visual representation please see the figure below:
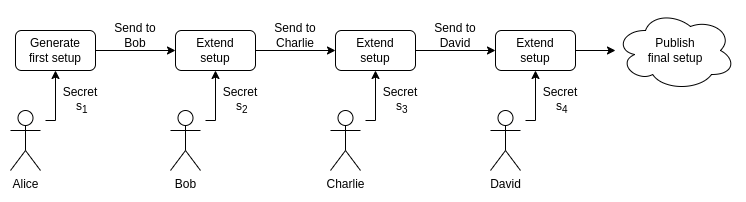
Further exploration of trusted setups can be found in Vitalik Buterin's comprehensive post on trusted setups.
poly
poly(data) → polynomial
Represents data as a polynomial needed for the rest of the scheme. The degree of the polynomial is equal to the (length of data - 1).
An ordered data set is treated as a set of values as (x,y) = (w^i, data[i]), where data[i] are SAFE_BYTES-byte (31 bytes) chunks, and w is a root of unity of degree , of from which a polynomial that satisfies for all these points is interpolated. This may be done every time needed using a saved root of unity (one field element).
The resulting polynomial is in coefficient form.
commit
commit(polynomial) → commitment
Computes a commitment to polynomial
create_witness
create_witness(polynomial, num_values, index) → witness
Computes a witness of evaluation of polynomial at index in the domain of size num_values
verify
verify(commitment, num_values, index, value, witness) → bool
Verifies that value is the evaluation at index of the polynomial in the domain of size num_values matching the commitment
Erasure Code
An erasure code extends given data according to its operation rate so that the original data can be recovered from a subset.
We currently use a Discrete Fourier Transform-based systematic Reed-Solomon code with a rate of 1/2 over the field , where is the size of subgroup of points BLS12-381 curve for the record chunks and the same approach over the subgroup of points for commitments.
The auxiliary parameters aux may include domain initialization for Fast Fourier Transform (FFT).
extend
extend(source_data, rate, aux) → extended_data
Extends source_data vector so that the result is 1/rate larger than the source using auxiliary parameters aux, as follows:
- interpolate a polynomial over the values in
datawith inverse FFT - read from
auxan evaluation domain of size double thesource_datalength - evaluate that polynomial over that larger domain to obtain
extended_datavector
recover
recover(data_shards, aux) → source_data
Recovers the original source_data if data_shards is at least rate the size of original data (i.e., half for the rate of 1/2) using auxiliary parameters aux.
We introduce counterparts to extend and recover functions specifically defined for the case of erasure coding the KZG commitments as elliptic curve points.
extend_commitments
extend_commitments(source_commitments, rate, aux) → extended_commitments
Extends source_commitments vector so that the result is 1/rate larger than the source using auxiliary parameters aux, as follows:
- interpolate a polynomial over the values in
source_commitmentswith inverse FFT - read from
auxan evaluation domain of size double thesource_commitmentslength - evaluate that polynomial over that larger domain to obtain
extended_commitmentsvector
In the extended data (for both records and commitments), the values with even indices (i.e., (0,2,…,254)) correspond to the source values and the values with odd indices (i.e.,(1,3,…,255)) correspond to parity values. The source data is effectively contained only in values with an even index, making it sufficient to obtain only those for direct recovery.
recover_poly
We introduce an additional function for efficient interoperation between KZG and RS:
recover_poly(partial_data, aux) → polynomial
Recovers the polynomial in coefficient form, which evaluates to data, without evaluating it, if partial_data is at least rate the size of original data (i.e., half if the rate is 1/2) using auxiliary parameters aux.
The resulting polynomial is suitable for use with the KZG primitives commit and create_witness.
- (Optimization, Implemented) The output of this function matches
KZG::Poly(Recover(partial_data))but it is faster due to computing 2 less FFTs, which saves time during time-sensitive Proving phase where we do not need to recover the source record data, but need to recover the corresponding polynomial coefficients to compute the KZG witness for winning chunk.
Encoding Mapping
Encoding provides a means to make arbitrary useful data (i.e. chunks of blockchain history) look like random data through encoding, while allowing to retrieve the useful data through decoding.
encode(data, key) → encoding
decode(encoding, key) → data
We currently use XOR as encoding function. The key in general may or may not depend on farmer public or private key.
Proof-of-Space
Proof-of-Space is used as an intermediary step in the construction of Proof-of-Archival-Storage consensus as a space-time tradeoff prevention mechanism. Proof-of-space is different from memory-hard functions in that the bottleneck is not in the number of memory access events, but in the amount of memory required.
For the more detailed specification of these primitives see Dilithium PoS Specification
generate
generate(k, seed) → pos_table
Initializes an amount of space larger than PIECE_SIZE by generating a Chia plot table from seed after forward propagation phase.
Currently, the space parameter k is set to 20 with resulting in 160-byte proofs-of-space.
The plot seed is obtained from farmer public key, current sector and piece offset within the sector.

find_proof
find_proof(pos_table, challenge_index) → proof_of_space
For a given challenge_index samples the pos_table for a valid full proof-of-space if the corresponding proof exists at this index, returns None otherwise.

is_proof_valid
is_proof_valid(k, seed, challenge, proof_of_space) ��→ bool
Verifies whether proof-of-space proof_of_space is valid for challenge of a table for k and seed.

