Proof-of-Space

This specification defines a secure proof-of-space construction for Plotting and Proving sub-protocols of the Dilithium consensus based on Chia PoS.

Parameters

• k: a global memory requirement parameter, currently 20
• seed: a unique 32-byte seed that determines memory contents (the table values) obtained from the farmer public key, current sector, piece offset within the sector and current history size.
• PARAM_EXT: a PRNG extension parameter to avoid collisions, currently 6
• PARAM_M = 1 << PARAM_EXT = 64 matching function parameter
• PARAM_B = 119 matching function parameter
• PARAM_C = 127 matching function parameter
• PARAM_BC = PARAM_B * PARAM_C matching function parameter

Table Generation

The table generation comprises computing seven tables $t_1, …, t_7$. Each table contains ~$2^k$ entries. The resulting tables are stored in memory.

The first table computes the outputs of $f_1(x)$, a stream PRNG, over the domain of possible $x$ indices $(0 \dots 2^k-1)$. The first table entries are pairs $(y_1 = f_1(x_i),\ x_i)$ sorted by value $y_1$ rather than by index. Sorting is needed to optimize matching in the calculation of the next table.

To compute the second table, we need to identify pairs of output values $y_1$ in the table $t_1$ that satisfy the matching function $M$. The entries for the second table are computed as outputs of $f_2(l =x_i,r=x_j)=hash(l||r)$ if and only if $M(f_1(x_i),f_1(x_j)) == True$. Imagine $M(l,r)= (l==r+1)$ (but it’s more complicated in reality).

To compute the third table, we need to identify pairs of output values $y_2$ in the table $t_2$ that satisfy the matching function $M$. The entries for the second table are computed as $f_3(l=(x_i,x_j),r=(x_k,x_l))=hash(l||r)$ if and only if $M(f_2(x_i,x_j),f_2(x_k,x_l)) == True$

And so on until the last table.

As a result, each entry in the tables $t_2, \dots, t_7$ stores the output of the respective $f_n(x)$ and a pair positions = (left_position, right_position) that points to two entries in the previous table such that a matching function is satisfied. The left_position is an integer indicating where the first match value is stored in the table $t_1$. The right_position is also an integer that indicates where the second match value is stored in the table $t_1$.

Final PoS Table Format

Table	Entries	Sorted by
Table1	y1=f1(x), x	y1
Table2	y2, metadata, pos1, offset	y2
Table3	y3, metadata, pos2, offset	y3
Table4	y4, metadata, pos3, offset	y4
Table5	y5, metadata, pos4, offset	y5
Table6	y6, metadata, pos5, offset	y6
Table7	y7, pos6, offset	y7

The entries in all tables are in the format (y, metadata, positions) with the last three optional. metadata is different from table to table. For the first table, the x values can be considered metadata .

generate

generate(k, seed) → pos_tables

Computes the 7 PoS tables.

1. Compute the first table t_1 = compute_table1(k, seed) and push to pos_tables.
2. Compute each of t_2, …, t_7, as follows, by table_number.
3. Take the previous table (table_number-1).
4. For each entry, separate the y values from the table entry into buckets (see illustration) in a sliding manner:

   1. Define two vectors of entries to hold two buckets of our sliding pair left_bucket and right_bucket. If this is not the first time we run this loop (we are not at the beginning of the table), set the current left_bucket to the previous right_bucket and continue. Otherwise:

      1. Take the entries entry.y while their bucket index left_bucket_index = entry.y/PARAM_BC is the same
      2. Place the entry into the first bucket left_bucket.push(entry).

   2. Take the next entries entry.y while their bucket index right_bucket_index = entry.y/PARAM_BC is the same as right_bucket_index == left_bucket_index + 1

   3. Place the entry into the second bucket right_bucket.push(entry)

   4. Find matches in between these buckets as a pair of indices, one from the first and one from the second bucket (left_index, right_index) = find_matches(left_bucket, right_bucket)

   5. For each matched pair (left_entry, right_entry) = (left_bucket[left_index], right_bucket[right_index]), compute the current table’s function (y, c) = compute_fn(table_number, left_entry.y, left_entry.metadata, right_entry.metadata)

   6. Map the match pair entries (left_entry, right_entry) positions back from the bucket to their respective positions in the previous table, left_position and right_position.

   7. Push to the current table an entry (ys, metadata, positions) = (y, c, {left_position, right_position})

   8. Sort the current table by (y, [left_position, right_position], metadata) value.

      • chiapos sorts the table by y, so the order may differ in our implementation.
      • chiapos uses k-way merge to deal with the fact that table might be too large to store in memory. Since we don’t have this problem we could use a faster algorithm.

The resulting pos_tables is a vector containing the 7 tables in order.

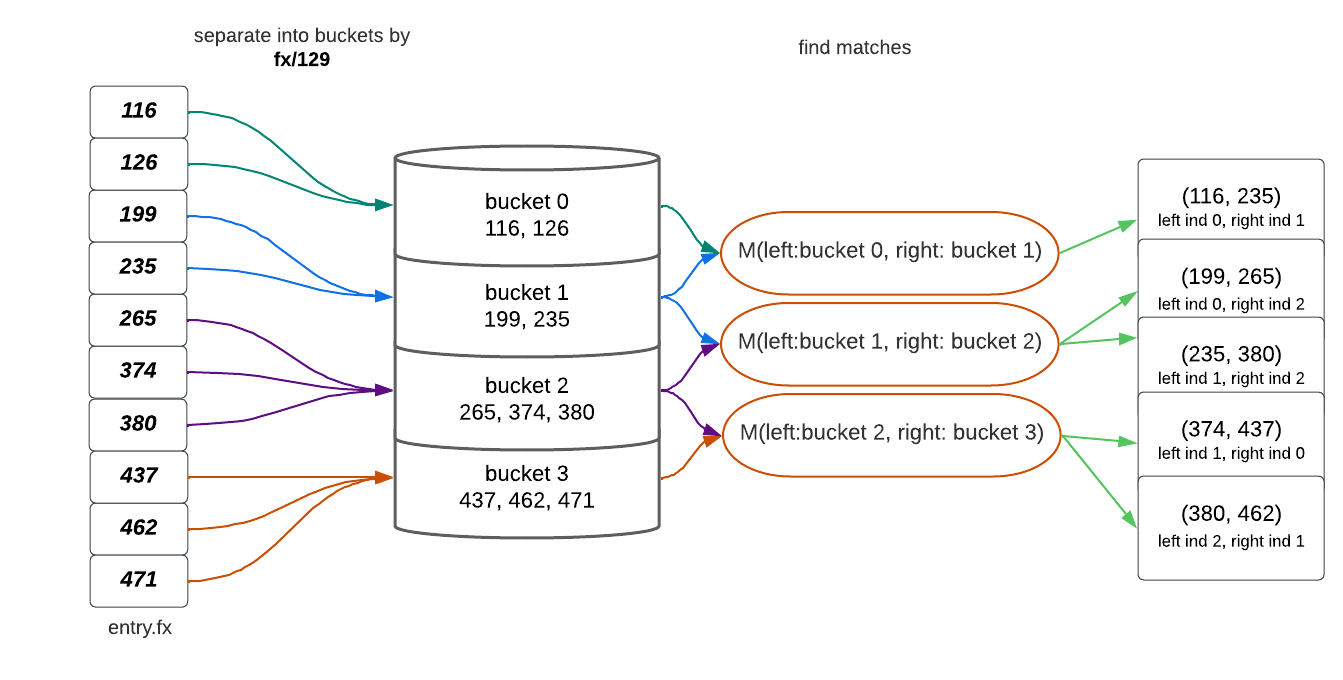
Steps 4.ii-iv in generate function definition. Numbers and matching function $M$ are solely illustrative. Since the entry.y is sorted, Chia does this sequentially on portions of the table as their tables don’t fit in memory. Notice that 235 and 380 appear in multiple matches, while some numbers don’t have a match.

Tables Computation

compute_table1

compute_table1(k, seed) → t_1

Computes the whole table t_1 for all values of x in 0..2^k:

1. Initialize ChaCha8 stream PRNG with the given seed ChaCha8(seed, 0).
2. Generate k*2^k bits of PRNG output. Slice it into 2^k fx values. The output for x=0 will be the first k bits, the output of x=1 will be the next k bits, and so on.
3. Append to each y the PARAM_EXT most significant bits of the corresponding x.
4. Push (y, x) pairs to t_1.
5. Sort t_1 by y.

• Consider this function a necessary optimization of compute_f1 It is much faster to generate the whole result of f1(0..2^k) in one go due to the stream nature of ChaCha instead of computing one by one. chiapos does in batches, since the whole table is too big in their case
• The output is extended by PARAM_EXT (6) bits, so f1(x) takes x of k bits as input and outputs y of k + 6 bits. These 6 bits are the most significant bits of x, added to minimize collisions (birthday paradox).
• Sorting is needed to optimize bucketing for find_matches in the calculation of the next table

compute_f1

compute_f1(k, seed, x) → y

Computes one value y for a specific x with the first table function. This is a version of compute_table1 but for a single value, necessary for the verifier that does not need to compute the whole table, only the selected `x`` values.

1. Compute skip_bits = x*k
2. Initialize ChaCha8 stream PRNG with the given seed ChaCha8(seed, 0).
3. Seek to the needed point skip_bits in the generated keystream.
4. Set y the next k bits from the keystream.
5. Append to y the PARAM_EXT most significant bits of x

This is a version of compute_table1 but for a single value, necessary for the verifier that does not need to compute the whole table, only selected x

The output y has length k+PARAM_EXT bits.

compute_fn

compute_fn(table_number, y_in, left, right) → (y, metadata)

1. Compute BLAKE3 hash hash = Hash(y_in || left || right)
2. y is hash truncated to k + PARAM_EXT bits
3. If table_number < 4 set metadata = left || right
4. If table_number >= 4 set metadata to hash bits [k+PARAM_EXT .. k+PARAM_EXT + metadata_size_bits(table_number)]

metadata_size_bits

metadata_size_bits(table_number) → size

Size of collation metadata corresponding to each table. Extra bits are added to each entry to make Hellman attacks more difficult and ensure that performing space-time tradeoffs is more expensive than honest table generation. For the first table, x value is considered metadata.

k * match table_number {

 1 => 1,
 2 => 2,
 3 | 4 => 4,
 5 => 3,
 6 => 2,
 7 => 0
    }

Matching Functions

The matching functions define whether two entries in a table match according to two conditions.

The first condition is that the 2 candidate entries belong to adjacent buckets.

The second condition is quite complex.

Consider an underlying graph of a table: the digraph where each node is an entry, and an edge exists if that pair of entries is a match. The second condition defines the edges of this graph for parameters PARAM_B and PARAM_C. Each node (entry) of this graph is described with a triplet $(i,b,c)$ for $i\in\Z$ (the bucket id of the entry), $b \in \Z_{PARAM\_B}$ (entry remainder modulo PARAM_B) and $c \in\Z_{PARAM\_C}$ (entry remainder modulo PARAM_C). The edges in the graph are given between two nodes as:

$(i, b, c) → (i + 1, b + m, c + (2m + i\%2)^2 )$

for all 0 ≤ $m$ < 64 = PARAM_M

The second condition avoids cycles between inputs if the set is represented as a graph. These cycles can be compressed by saving fewer entries and deriving the rest, representing a potential attack because it would optimize storage (see Cycles Attack in Chia Proof-of-Space Construction v1.1-1). This is also why PARAM_B = 119 and PARAM_C = 127 have those values.

get_left_targets

get_left_targets() → left_targets

Compute possible target matching values left_targets for use in find_matches that fulfill the second condition of the matching function. Note that this only needs to be done once for a set of PARAM_* constants, not on every call:

1. Iterate over parity in 0..=1
   1. Iterate over bc in 0 .. PARAM_BC
      1. Calculate c as i/PARAM_C
      2. Iterate over m in 0 .. PARAM_M
         1. Calculate yr as ((c + m) % PARAM_B) * PARAM_C + (((2 * m + parity)^2 + bc) % PARAM_C);
         2. Set left_targets[parity][bc][m] = yr

left_targets can be a global value.

find_matches

find_matches(left_bucket, right_bucket) → vec((left_index, right_index))

Given two buckets with entries (y values), computes which y values match and returns a list of the pairs of indices (left_index, right_index) into left_bucket and right_bucket.

Instead of doing naive pair-wise comparison in $O(N^2)$ we first compute the target values needed to match based on left bucket, then scan the right bucket

1. Iterate over entries in right_bucket by right_index.

   1. Create rmap that will store a mapping from r to a list of right bucket positions.
   2. Reduce each entry value to the remainder of its division by PARAM_BC. To do so, compute r_base = (right_bucket[0].y/PARAM_BC) * PARAM_BC and subtract it from each entry’s fx in the right bucket to get r = entry.y - r_base.
   3. Since the same fx and, as a result, the remainder r can appear in the table multiple times, in which case they'll all occupy consecutive slots in right_bucket. Hence, all we need to store in rmap is just the position right_index of the first appearance of each r and the number of elements in a map at rmap[r].

   y is not unique, so multiple right_index can match the same rmap[r], but they will all be next to each other, so it is possible to store start index and count rather than dynamically sized vector of indices.

2. Calculate the parity (0 or 1) of the first entry in left_bucket as (left_bucket[0].y/PARAM_BC)%2.

3. Iterate over entries in left_bucket with left_index being the index of the corresponding entry.

   1. Reduce each entry value to the remainder of its division by PARAM_BC. To do so, compute l_base = r_base - PARAM_BC and subtract it from each entry’s fx in the left bucket to get r = entry.y - l_base.

      For each left_bucket entry m, set a target value r_target as left_targets[parity][r][m]

   Check rmap[r_target] for right indices and collect into pairs of (left_index, right_index).

4. Return the list of all matching pairs.

Find Quality

Note: Not used in Dilithium, used only for testing the implementation against Chia.

Quality is a 32-byte hash of 2 table entries within the 64-entry full proof. This value is known in the Chia context as a proof quality string however, this naming is irrelevant to our use case as we do not assign any qualitative measure to the outputs of the PoS table.

On the verifier side, the quality is extractable from the full proof.

This value is known in the Chia context as a proof quality string; however, this naming is irrelevant to our use case as we do not assign any qualitative measure to the outputs of the PoS table.

find_quality

find_quality(pos_table, challenge) → proof_quality / None

For a given challenge , sample the pos_table for a proof-of-space quality string the corresponding proof exists at this index, and return None if it doesn’t.

1. Take all the entries in the last table t_7.
2. Scan the entries’ entry.y values to find one where the first k bits match the first k bits of the challenge. If it doesn’t exist, return None.
3. Take the last 5 bits last_five_bits of the challenge to determine the path to follow.
4. For the matching entry in t_7, iterate backward over tables t_6 .. t_2 and backward over last_five_bits:
   1. If the corresponding bit in last_five_bits is 0, read the new entry in the current table at the position entry.left_position
   2. Else if the corresponding bit in last_five_bits is 1, read the new entry in the current table at the position entry.right_position
   3. Perform the same read in the previous table for the newly found entry
5. After step 3 finishes by reaching the second table t_2, read 2 entries in the first table:
   1. Read the left_entry in t_1 at the position entry.left_position
   2. Read the right_entry in t_1 at the position entry.right_position
   3. Add the left and right entries to the quality_entries vector.
6. For the two entry in quality_entries, take entry.x truncated to k bits and concatenate them together.
7. Output the 32-byte SHA256 hash of challenge || left_entry.x || right_entry.x .

• Generally a path to chose between left entry and right entry depends on last bits of challenge (left if 0, right if 1), but we set them all to 0 so we can always follow the entry corresponding to position

Proving

A proof-of-space for a given challenge is a set of 64 k-bit entries of table t_1.

To find proof, we must see if table t_7 has one or more entries entry.y values where the first k bits match the first k bits of the challenge. Each satisfying entry in the last table, t_7, points to 2 entries in table t_6. These two entries will point to 2 entries in table t_5 and so on up to table 1. So an entry in the last table will indirectly point to 64 entries in the first table ($2^{7−1}$ ). These 64 entries concatenated are the proof-of-space.

find_proof

find_proof(pos_table, challenge) → proof_of_space

For a given challenge, query the pos_table for a valid full proof-of-space.

1. Take all the entries in the last table t_7
2. Scan the entries’ entry.y values to find one where the first k bits match the first k bits of the challenge.
3. For the matching entry in t_7, iterate backward over tables t_6 .. t_1
   • Set an empty entries_buffer
   • Read the left_entry in the current table at the position entry.left_position.
   • Read the right_entry in the current table at the position entry.right_position
   • Add the left and right entries to the entries_buffer vector.
   • Perform the same read in the previous table for each newly found entry in the buffer.
4. After step 3 finishes by reading all required entries from the first table t_1, the entries_buffer should have 64 entries.
5. For each entry in entries_buffer, take the corresponding entry.x and concatenate them together.

Verification

Verification of the 64-point proof-of-space is performed by evaluating the table functions f1..fn on each x in the proof and checking whether they satisfy the matching function at each step.

To verify a proof-of-space, we need 4 things: the 64 x values in the proof_of_space, the parameter k, the seed, and the challenge_index. The process is more or less the same as table generation, i.e., we compute the same functions but do not generate the entire tables, only a tiny subset. Only the outputs for the x values of the proof are calculated to be able to verify that:

1. the outputs f1..f7 satisfy the matching function at each step,
2. the final output fn of table t_7 corresponds to the challenge_index.

Consider an example with four tables. The proof-of-space then consists of $2^{(4-1)} = 8$ values $x_1||…||x_8$. The verifier will perform the following:

1. Compute the outputs of the first table function $f_1(x)$:

$f_1(x_1), f_1(x_2), f_1(x_3), f_1(x_4), f_1(x_5), f_1(x_6), f_1(x_7), f_1(x_8)$

2. Verify that the matching function $M$ returns a match on each of the following four pairs

$M(f_1(x_1), f_1(x_2)), M(f_1(x_3), f_1(x_4)), M(f_1(x_5), f_1(x_6)), M(f_1(x_7), f_1(x_8))$

3. Compute the outputs of the second table function $f_2(x)$:

$f_2(x_1, x_2), f_2(x_3, x_4), f_2(x_5, x_6), f_2(x_7, x_8)$

4. Verify the matching function $M$ returns a match on each of the following two pairs

   $M(f_2(x_1, x_2), f_2(x_3, x_4)), M(f_2(x_5, x_6), f_2(x_7, x_8))$

5. Compute the outputs of the third table function $f_3(x)$:

   $f_3((x_1, x_2), (x_3, x_4)), f_3((x_5, x_6), (x_7, x_8))$

6. Verify the matching function $M$ returns a match

   $M(f_3((x_1, x_2), (x_3, x_4)), f_3((x_5, x_6), (x_7, x_8)))$

7. Compute the last table value

   $fx =f_4((x_1,x_2,x_3,x_4),(x_5,x_6,x_7,x_8))$

8. Verify this value corresponds to our challenge $truncate(fx) = challenge\_index$

is_proof_valid

is_proof_valid(k, seed, challenge, proof_of_space) → bool

Verifies whether proof-of-space proof_of_space is valid for the challenge of a table for space_k and seed.

1. Split proof_of_space into k-bit x_values. Check that x_values has length 64.
2. Set 2 empty vectors for y_values and metadata.
3. For each x in x_values:
   1. Calculate the (y, x) = compute_f1(x) value for each x, and add the y value and x metadata to the y_values and metadata vectors, respectively.
4. Iterate over table numbers 2..=7:
   1. Iterate over y_values and metadata in steps of 2 (for left and right entries)
   2. Create left_entry and right_entry structs from the y_values and metadata.
   3. Adding left_entry to left_bucket and right_entry to right_bucket vectors
   4. Check that find_matches returns exactly 1 match. If not, the verification failed.
   5. Calculating compute_fn(table_number, left_entry.y, left_entry.metadata, right_entry.metadata) and push to buffer.
   6. Set y_values and metadata to the buffer vectors.
5. Check that the first k bits of y_values[0] match the first k bits of challenge_index.

• Verification is fast, but not quite fast enough to be verified in Solidity on Ethereum (something that would enable trustless transfers between chains), since this verification requires blake3 and chacha8 operations.